Table of Contents
Decoding bitstreams for fun and profit
by lft
This article describes a technique for extracting bitfields from a long sequence of bytes stored in RAM.
As an example application, consider a scroller where the text is a string of 5-bit character codes. The entire text could then be stored as a bitstream, from which you read five bits at a time. But you might save some space if you represent, say, the eight most common characters as 0xxx, and all other characters as 1xxxxx. (This would also give you 40 different characters, rather than 32.) In that case, you'd first want to read a 1-bit field, to differentiate between the two cases. Then you'd read either a 3-bit field or a 5-bit field.
We will discuss how to do this efficiently and elegantly on the 6502. In particular, we will look at a technique that performs the two-stage procedure described above, and even navigates arbitrary decision trees, as part of its normal operation.
The schoolbook application for this kind of routine would be a Lempel-Ziv-Welch decruncher or a Huffman decoder. But anything is possible! For instance, you could use it to parse note events in a playroutine, instructions in a virtual machine, or entropy encoded sound samples.
We will start with a simple design, and then add complexity step by step, also optimising it to the point where the complete decoder is quite devilish to follow.
From bytes to bits
At the heart of the bitfield decoder is the shifter. This is essentially a mini-buffer of pending bits, represented as a single byte in the zero-page. As we shift out bits, the buffer occasionally becomes empty, at which time a new byte is loaded into it. The clever part is how we represent the shifter. This is an old established technique, but it can be rather baffling when you see it for the first time.
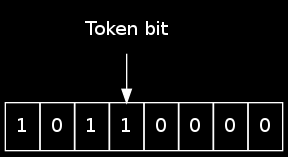
The idea is that the shifter contains (from left to right) 0–7 bits of pending data, followed by a single 1-bit that we'll refer to as the token, followed by zeros. So, the following shifter contains three bits of data (1, 0, 1):
At program start, the shifter is initialised to $80.
Here is a first attempt at a getbit routine:
getbit
asl shifter
bne done
jsr getbyte
sta shifter
sec
rol shifter
done
; The bit is now in C.
rts
In order to read a bit from the shifter, we first perform an ASL. Normally, this puts one bit of data in the carry flag, while also preparing the shifter for the next bit. But if the Z flag was set by the ASL, the buffer was in fact empty, and we shifted out the token bit. In that case, we grab a new byte, store it in the shifter, and then ROL to get the first data bit from the new byte. The ROL will also shift in a new token bit.
In practice, it would be slow to call a subroutine in order to fetch new bytes. After all, this will happen for every eighth bit, which is quite often. Instead we'll use some self-modifying code, and keep a pointer to the next byte inside an instruction operand, like this:
getbit
asl shifter
bne done
mod_source
ldx buffer
inc mod_source+1
bne no_new_page
inc mod_source+2
no_new_page
stx shifter
rol shifter
done
; The bit is now in C.
rts
We're using the X register because we're going to need A for something else soon.
Note that the SEC has now been removed, because carry is already set from the previous token bit. If you want to get philosophical about it, you might say that it's “the same” token bit that gets re-used over and over.
Next, we will rearrange the code to reduce the number of branch-taken penalty cycles. From now on, we must make sure to CLC before calling getbit.
getbyte
mod_source
ldx buffer
inc mod_source+1
bne no_new_page
inc mod_source+2
no_new_page
stx shifter
getbit
rol shifter
beq getbyte
; The bit is now in C.
rts
From bits to fields
So now we can read individual bits from the stream. Let's pack them together into bitfields!
We could of course call the getbit routine from a loop:
getfield
; Y contains the requested number of bits
lda #0
clc
field_loop
jsr getbit
rol
dey
bne field_loop
; The bitfield is now in A.
rts
(This is why we had to preserve the A register during getbit/getbyte.)
But again, subroutine calls are costly, so we'll merge getfield and getbit into a single routine. However, getting a single bit is now slower, because we have to treat it as a field of size one.
getbit
ldy #1
getfield
; Y contains the requested number of bits
lda #0
clc
jmp field_loop
getbyte
mod_source
ldx buffer
inc mod_source+1
bne no_new_page
inc mod_source+2
no_new_page
stx shifter
field_loop
rol shifter
beq getbyte
rol
dey
bne field_loop ; C is clear
rts
Note that, because we clear A at the beginning, we don't have to CLC before
looping back to field_loop.
But we can do better than this! Instead of representing the requested number of bits as an integer in the Y register, we can represent it as a single 1-bit in the accumulator. As we shift new data into the accumulator, the 1-bit gets closer and closer to the MSB, and when it finally falls off the edge, we terminate the loop:
getbit
lda #%10000000
getfield
; Position of 1-bit in A represents requested number of bits
clc
jmp field_loop
getbyte
mod_source
ldx buffer
inc mod_source+1
bne no_new_page
inc mod_source+2
no_new_page
stx shifter
field_loop
rol shifter
beq getbyte
rol
bcc field_loop
rts
This preserves Y and saves two cycles per bit (DEY).
Two-stage fields
Given the above routine, we are now in a position to implement the scroller scenario described in the introduction. Here is some code to fetch a new character from the bitstream:
getchar
jsr getbit
bne large
; 3-bit character code
lda #%00100000
jmp getfield
large
; 5-bit character code
lda #%00001000
jsr getfield
clc
adc #8
rts
Actually, we can shave off a byte and a pair of cycles by recognising that getfield always returns with carry set: We can safely omit the CLC and do ADC #7 instead.
In more complex scenarios, such as decrunchers, we often need to distinguish between more than two cases. Perhaps we read two bits in order to select between four differently-sized encodings:
| Value range | Coded as | Value offset (what to add to x) |
|---|---|---|
| 0-1 | 00x | 0 |
| 2-5 | 01xx | 2 |
| 6-21 | 10xxxx | 6 |
| 22-149 | 11xxxxxxx | 22 |
Rather than spelling out these four cases as different paths through the code, we can use a table-based approach. This helps keep down the size of the decruncher, which is often very important. It will also enable some more optimisations further down the rabbit hole.
We will use one table for the field widths, and one table for the value offsets.
getvalue
lda #%01000000 ; Get two bits.
jsr getfield
tay
lda fields,y
jsr getfield
clc
adc offsets,y
; 9-bit value returned in A and C.
rts
fields
.byt %10000000 ; Get one more bit.
.byt %01000000 ; Get two more bits.
.byt %00010000 ; Get four more bits.
.byt %00000010 ; Get seven more bits.
offsets
.byt 0
.byt 2
.byt 6
.byt 22
Note that in the example, the maximum value returned is 149. Therefore, rather than saying that the result is a 9-bit value, we could simply say that the routine returns with carry undefined, and with an 8-bit result in A. We could then eliminate the CLC, and compensate by subtracting one from each value in the offset table. The reason why we can't do this for 9-bit values, is that the first entry in the offset table would become $ff, and this would cause values 0 and 1 to instead come out as 256 and 257.
Decoding with arbitrary decision trees
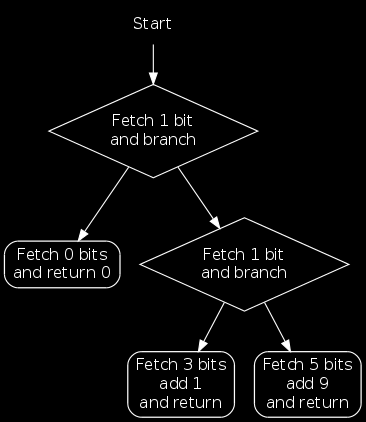
Consider again our scroller example. Suppose we wish to encode a particularly common character (such as space) using a single bit. We might decide on the following encoding scheme:
| Value range | Coded as | Value offset (what to add to x) |
|---|---|---|
| 0 | 0 | 0 |
| 1-8 | 10xxx | 1 |
| 9-40 | 11xxxxx | 9 |
To fetch a character now, we start by getting a single bit. Based on the value of this bit, we're either done or we fetch one more bit. Based on this bit, we then either fetch three or five bits.
This algorithm is essentially a tree of decisions, as illustrated by the following flowchart:
We will refer to the rhombus-shaped nodes as branch nodes and the rounded-rectangle nodes as return nodes.
Such decision trees are usually implemented explicitly, as code. But for large trees, the decoder becomes unwieldy. Next up, we'll see how we can represent decision trees more compactly using tables.
In each node of the flowchart above, we first fetch a bitfield (possibly of size zero), and then either:
- Branch to a different node, or
- Add a constant and return.
It is time to introduce another decoding trick! So far, the field specifiers (what we put in A prior to calling getfield) have consisted of a number of zeros followed by a single set bit. But the remaining bits have no purpose yet, and they will be available in A when getfield returns, shifted into a position immediately to the left of the fetched bits.
So, if we call getfield with A set to 001ttttt (t is for tag), we'll get
tttttxxx back, where x is the fetched bitfield.
The most significant bit of the tag will also be in the sign bit of the status register. Some decrunchers, e.g. Doynamite, use this to determine whether the value returned is complete, or whether it's just the high-byte of a larger value. In the latter case, the low-byte can be grabbed very quickly straight from the byte stream. Essentially, one tag bit is used to differentiate between two cases.
However, in the present technique, we wish to encode a generic decision tree, and for this we'll have to use more tag bits.
(In the following, the word “branch” will refer to branches in the flowchart, not 6502 branch instructions!)
Suppose we put a number on each node in the flowchart. The current node number will be kept in the Y register. From this number, we can deduce (using a lookup table) how many bits to fetch, whether we should branch or return after fetching, and—in case of a branch node—what range of nodes we should branch to.
All of this information can be encoded as a single byte, and placed in the accumulator before calling getfield. As we have already seen, the number of leading zeros determines the field width. They are followed by a single set bit and a tag. We will use the most significant tag bit to keep track of what kind of node we're in. If this bit is clear, we're in a branch node, in which case the remaining tag bits will be used to encode the range of branch targets.
A separate lookup table, also indexed by the current node number in Y, will be used to hold the constants that are added in return nodes.
decode
ldy #4 ; Start at node 4, the last node in the table.
decode_loop
; Y represents the current node, and is an index into the field and
; offset tables.
lda fields,y
; In A, we now have:
; a number of zero bits, controlling how many bits to fetch
; a one bit
; if we are in a return node:
; a one bit (tag MSB)
; fill up with zeros
; if we are in a branch node:
; a zero bit (tag MSB)
; tag bits --> first target node (after shift)
; Special exception to the above:
; If we're going to fetch a zero-length field, A is zero.
; Handle that now.
beq done
; Otherwise, fetch the field.
jsr getfield
; In A, we now have:
; a bit indicating whether we are in a branch or return node
; more tag bits (all zero in case of a return node)
; the field we just fetched
; Are we in a return node?
bmi done
; No, this was a branch node. The branch target is in A.
; Note that the target has been constructed automatically by
; concatenating the tag with the fetched bits. So if the tag was 0011
; and we fetched 101, we're going to branch to node 0011101.
tay
jmp decode_loop
done
; Add constant and return.
clc
adc offsets,y
rts
fields
.byt %00000000 ; Node 0: Fetch no more bits.
.byt %10000001 ; Node 1: Fetch 1 bit, then branch to node 2/3.
.byt %00110000 ; Node 2: Fetch 3 bits, then return.
.byt %00001100 ; Node 3: Fetch 5 bits, then return.
.byt %10000000 ; Node 4: Fetch 1 bit, then branch to node 0/1.
offsets
.byt 0 ; Add constant to obtain range 0-0.
.byt 0 ; Unused (branch node)
.byt $80+1 ; Add constant to obtain range 1-8.
.byt $80+9 ; Add constant to obtain range 9-40.
.byt 0 ; Unused (branch node)
A subtlety is that when we return without fetching anything (node 0), the accumulator will be zero before adding the constant. Otherwise, the accumulator will be $80, and we have to compensate accordingly in the offset table.
The above code was organised for clarity. However, we can rearrange the loop to eliminate the JMP instruction. There's also no need to start by setting up a constant Y, as we could just as well load A directly. Since the first node is always a branch node, we won't be using Y after the fetch, so we can leave it uninitialised. Hence:
decode
lda #%10000000 ; Fetch 1 bit, then branch to node 0/1.
decode_loop
jsr getfield
bmi done
tay
lda fields,y
bne decode_loop
done
clc
adc offsets,y
rts
fields
.byt %00000000 ; Node 0: Fetch no more bits.
.byt %10000001 ; Node 1: Fetch 1 bit, then branch to node 2/3.
.byt %00110000 ; Node 2: Fetch 3 bits, then return.
.byt %00001100 ; Node 3: Fetch 5 bits, then return.
offsets
.byt 0 ; Add constant to obtain range 0-0.
.byt 0 ; Unused (branch node)
.byt $80+1 ; Add constant to obtain range 1-8.
.byt $80+9 ; Add constant to obtain range 9-40.
The CLC at done can be removed if we adjust the offset table: We subtract one
from each table entry that corresponds to a return node where a non-zero-sized
field was fetched.
Putting it all together
Cramming an arbitrary decision tree into the field table is all very nifty, and it keeps down the size of the decoder considerably. But what about performance? Surely, putting a flowchart in a table can't be faster than simply coding it with explicit branch instructions?
But as a consequence of the table-driven design, there is now a great optimisation opportunity staring us in the face: We're down to a single call to the getfield routine, and that means we can inline it!
decode
lda #%10000000 ; Fetch 1 bit, then branch to node 0/1.
clc
jmp decode_loop
getbyte
mod_source
ldx buffer
inc mod_source+1
bne no_new_page
inc mod_source+2
no_new_page
stx shifter
decode_loop
rol shifter
beq getbyte
rol
bcc decode_loop
bmi done
tay
lda fields,y
clc
bne decode_loop
done
; Carry will be set if we got here via the BMI, i.e. after fetching a
; non-zero-sized field. Compensate in the table.
adc offsets,y
rts
fields
.byt %00000000 ; Node 0: Fetch no more bits.
.byt %10000001 ; Node 1: Fetch 1 bit, then branch to node 2/3.
.byt %00110000 ; Node 2: Fetch 3 bits, then return.
.byt %00001100 ; Node 3: Fetch 5 bits, then return.
offsets
.byt 0 ; Add constant to obtain range 0-0 (Carry clear).
.byt 0 ; Unused (branch node)
.byt $7f+1 ; Add constant to obtain range 1-8 (Carry set).
.byt $7f+9 ; Add constant to obtain range 9-40 (Carry set).
Indeed, with such a flexible routine, one might even be able to drive all decoding from a single call site, and thus to inline the call to the decoder itself. For a real-world example of this, please have a look at the decruncher in Spindle 2.1.
A final touch
The code is already looking rather streamlined, but let's top it off with one
more optimisation: We can get rid of two cycles for each step through the
decision tree, by eliminating the CLC right before branching back to
decode_loop.
The following trick is only possible if, for each node, the number in the field table is either zero (for a zero-size fetch) or strictly larger than the node number. Many decision trees have this property, because node numbers are small integers, while numbers in the field table tend to be large. If not, it may be possible to fix it by rearranging the node numbers.
The idea is to access the table a little differently: Instead of simply loading from it, we perform an ADC. Naturally, we then have to compensate in the table, by subtracting from each element the node number (which happens to be in A at the time of the addition) and 1 (for the carry flag, which is set).
With that, we are ready for the final version of the decoder. It is listed below in the form of a subroutine, but, as mentioned earlier, it should be inlined for maximum performance.
decode
lda #%10000000 ; Fetch 1 bit, then branch to node 0/1.
clc
jmp decode_loop
getbyte
mod_source
ldx buffer
inc mod_source+1
bne no_new_page
inc mod_source+2
no_new_page
stx shifter
decode_loop
rol shifter
beq getbyte
rol
bcc decode_loop
bmi done
tay
adc fields,y
bne decode_loop ; Carry is clear when branching.
done
; Carry is set.
adc offsets,y
rts
fields
.byt %00000000-0-1 ; Node 0: Fetch no more bits.
.byt %10000001-1-1 ; Node 1: Fetch 1 bit, then branch to node 2/3.
.byt %00110000-2-1 ; Node 2: Fetch 3 bits, then return.
.byt %00001100-3-1 ; Node 3: Fetch 5 bits, then return.
offsets
.byt $ff ; Add constant to obtain range 0-0.
.byt 0 ; Unused (branch node)
.byt $7f+1 ; Add constant to obtain range 1-8.
.byt $7f+9 ; Add constant to obtain range 9-40.
Conclusion
We have seen how to extract bitfields from byte sequences stored in RAM, using a highly efficient technique that is capable of navigating arbitrary decision trees as part of the decoding process.